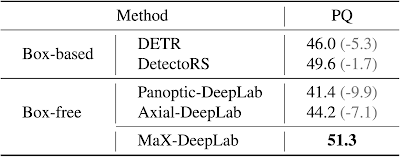
As robots become more ubiquitous in day-to-day life, the complexity of their interactions with each other and with the environment grows. In a controlled environment, such as a lab, multiple robots can coordinate their actions and efforts through a centralized planner that facilitates communication between individual agents. And while much research has been done to address reliable sensor-informed goal navigation, in many real-world applications aligning goals across independent robotic agents must be done without a centralized planner, which poses non-trivial challenges.
An example of such a challenging decentralized task is the rendezvous task, in which multiple agents must agree upon a time and place at which they can meet, without explicitly communicating with one another. This goal alignment task plays an important role in real world multiagent and human-robot settings, e.g., performing object handovers or determining goals on the fly. Solving the decentralized rendezvous task in this situation depends not just on the obstacles in the environment, but also the policies and dynamics of each agent. Addressing potential miscoordination and dealing with noisy sensor data depends on the agents’ ability to model the motions of other agents as well as their own, and to adapt to diverging intentions while using limited information.
In “Model-based Reinforcement Learning for Decentralized Multiagent Rendezvous”, presented at CoRL 2020, we propose an holistic approach to address the challenges of the decentralized rendezvous task, which we call hierarchical predictive planning (HPP). This is a decentralized, model-based reinforcement learning (RL) system that enables agents to align their goals on the fly in the real world. We evaluate HPP in a mixture of real-world and simulated environments and compare it to several learning-based planning and centralized baselines. In those evaluations, we show that HPP is able to more effectively predict and align trajectories, avoid miscoordinations, and directly transfer to the real world without additional fine-tuning.
Putting Together Prediction, Planning and Control
Akin to a standard navigation pipeline, our learning-based system consists of three modules: prediction, planning, and control. Each agent employs the prediction model to learn agent motion and to predict the future positions of itself (the ego-agent) and others based on its own observations (e.g., from LiDAR and team position information) of other agents’ behaviors and navigation patterns. So, each agent learns two prediction models, one for its own motion and one for the other agent. These motion predictors constitute the prediction module, and are used by each agent’s planning module.
The output of the prediction module — the estimate of where each agent, both the ego-agent and the other agents, is most likely to be given the ego-agent’s own sensor observations — is useful information for the planning module, which evaluates different goal locations and maintains a belief distribution over where the team should converge. The belief distribution is periodically updated using evaluations provided by the prediction model. An agent samples from this belief distribution to update the goal to which it should navigate.
The selected goal is passed to the agent’s control module, which is equipped with a pre-trained, imperfect navigation policy that can navigate to a given location in the obstacle-laden environment. The control policy then determines what action the robot should execute.
This process of observing other agents, updating belief distributions and navigating to an updated goal repeats until agents have successfully rendezvoused. While the hierarchical planning and control setup are not unusual, our work closes the loop between the control and planning for decentralized multiagent systems by use of the sensor-informed prediction module.
Training the Prediction Models
HPP trains motion predictors in simulation, assuming that each agent is controlled by a hidden, perhaps suboptimal, control policy capable of avoiding obstacles. The key difficulty lies in training prediction models without access to other agents’ sensor observations and control policies.
The predictors are trained via self-supervision. To collect the training data, we randomly place all the agents and obstacles in an environment, and each agent is given a random goal (unknown to other agents). As the agents move toward their respective goals, each agent records the experience — its sensor observations and the poses of all agents (itself and other agents). Next, from the recorded experience, the agent learns a separate predictor for each agent in the team including itself (target agent). The training dataset consists of ego-agent initial sensor observations, target agent’s pose and goal, labeled with future ego-observations and target agent poses. The goal and labels are inferred from the recorded experience.
As a result, the predictors learn temporal causality of the present and future ego-agent’s observations and target agent’s poses, conditioned on the target agent’s assumed goals — in other words the models predict where each agent will be in the future based on the present. The predictor training is done only with the information available to agents at the runtime, and in environments independent from the deployment environments.
Selecting Goals for Alignment
A model-based RL planner for each agent uses the learned predictors in the deployment environments to guide the agents towards the rendezvous point. The planner takes into account what it believes the other agents would do when also completing the rendezvous task.
 |
| HPP illustration. Each robot independently considers several potential rendezvous points, and evaluates each point based how close it believes that the agents can get. |
To perform this reasoning, each agent independently samples a series of potential goals and selects the goal that it believes it would be the most likely to succeed. This process effectively simulates a centralized planner for fictitious agents by using the prediction models to predict trajectories of those agents moving to a fixed goal. Conditioned on a proposed goal, the algorithm predicts the poses of the agents in the future, which are generated from sequential roll outs of the prediction models. Each goal is then evaluated by scoring the anticipated system state using the task reward favoring goals that bring agents closer together. We use the cross-entropy method (CEM) to convert these goal evaluations into belief updates over potential rendezvous points. Finally, the agent’s planner selects a goal for itself from this new belief distribution and passes this goal to the agent’s control module.
Results
We compare HPP against several baselines — MADDPG (learning-based), RRT (planning) with CEM, and centralized baselines that use heuristics for selecting the agent’s rendezvous point — in a mixture of real-world and simulated environments.
 |
| Evaluation environments, each of which are independent of the training environment for the agent’s control policy and prediction modules. |
There are two main takeaways from our results. One is that HPP enables agents to predict and align trajectories, avoiding miscoordinations. For example:
The second takeaway is that HPP transfers directly into the real world without additional training. For example:
Conclusion
This work presents HPP, a model-based RL approach for decentralized multiagent coordination. Agents first learn to predict where they and their teammates are going to be from their own sensors and decide and navigate to a common goal. Our experiments demonstrate the method generalizes to new environments and handles miscoordination while making no assumptions about the dynamics of other agents. This may be of interest to the larger multiagent research community as a real-world example of a decentralized task using noisy sensors and imperfect controllers, to the motion planning community as an example of a learning-based planning system that closes the loop between the planner and controller, and to the RL community as an example of model-based RL as feedback in a hierarchical, self-supervised prediction setting.
Acknowledgements
This research was done by Rose E. Wang, J. Chase Kew, Dennis Lee, Tsang-Wei Edward Lee, Tingnan Zhang, Brian Ichter, Jie Tan, Aleksandra Faust with special thanks to Michael Everett, Oscar Ramirez and Igor Mordatch for the insightful discussions.